Posted in Uncategorized

The must NOT have Windows 8 Start Menu Group Policy Setting

   02/03/2012  32 Comments

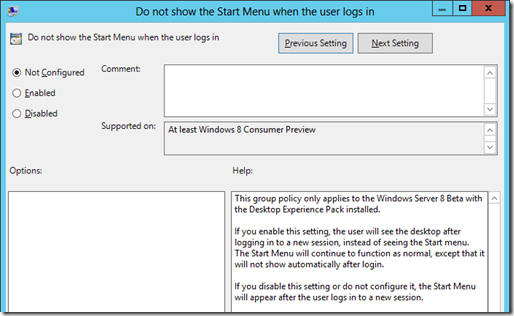
prod_Windows8CP_heroSo unless you have been under a rock for the past 24 hours then you would have missed the public release of Windows 8 Consumer Preview and Windows Server 8 Beta. I have only been running less than 24 hours and I am finding heaps of new exciting Group Policy settings that I will blog about soon but one really stands out. The “Do not show the Start Menu when the user logs in” policy allows you to boot the OS into the more familiar desktop and not the Metro start menu. Interesting to note that booting into the desktop is also the default behaviour for Windows Server 8 so you can also use this setting on your server if you want to start them into Metro (but you prob don’t want to).

This setting can be found under User Configuration > Policies > Administrative Templates > Start Menu and Taskbar and of course only work on Windows 8 Consumer Preview.

image

Update: I have tested this policy setting and it appears it does not work on the Windows 8 Consumer Preview. I suspect this is a bug as the Supported On statement clearly says “Windows 8 Consumer Preview”.


Update #2 / Rant: OMG! In closer look at the help of the setting it says “this group policy only applies to the Windows Server 8 Beta”  meaning that Microsoft are deliberately forcing people to launch the start menu. The fact that this is NOT something that can be controlled is VERY frustrating a reeks of an Apple like attitude of telling us that is not something we want. I get that the default is to launch into the metro start menu and I even think it is a better menu than the traditional start menu. But taking away people’s choice to go straight to the desktop is going to anger a lot people like myself especially when we know it is a Server OS option.

 

Share:

Author: Alan Burchill

Microsoft MVP (Group Policy)

32 thoughts on “The must NOT have Windows 8 Start Menu Group Policy Setting”

  12. Definitely will be useful for enterprise computer setups, but I actually began to enjoy new Start Screen after proper customization of tiles and shortcuts of course!

    Reply

    1. Yes… looks like it does not work… Have put in an update. But it does clearly say that Consumer Preview is supported so i suspec this is a bug.

  14. There are other GPO settings that have incorrect “Supported on” information but as this GPO clearly state “This setting only applies to Windows Server 8 beta” means that is a political decision to not make this setting available on the client.

    Reply

  15. I see no issue with this from a user or admin perspective. The start screen is a great place to dump users afte login as it gives them quick access to their applications. The policy is only for servers with the desktop experience pack…ie those setup as a RDS/terminal server…so again this is not really an issue and is more likely something for those who want to host their terminal servere on Server 8 but have a majority XP/7 user base.

    Reply

  17. wizmo on the desktop really helps – metro sux all cluttered and icons jumping everywhere . . . no damned good on a desktop! vistart give you a start menu too, makes win 8 tolerable . . . I need a desktop not a bloody tablet . . .

    Reply

  18. I wrote about this setting back when the Windows Developer Preview was released – it didn’t work in that version, either: http://blog.quppa.net/2011/09/15/windows-8-bypassing-the-start-screen/

    The ‘Windows Server 8 Beta’ text can be interpreted in another way: for the setting to work in Windows Server 8, the Desktop Experience Pack must be installed. Those components are already present in client versions of Windows, so it should work out of the box for non-server computers. I’m disinclined to download a copy of the Windows Server 8 Beta, but I’d be interested to know if the setting has any effect in that version.

    Reply

  19. Microsoft shouldn’t force the metro UI onto non-tablet users.
    The lack of choice (with GPO or regular setting) for the classic start menu/desktop will not help corporate adoption of Windows 8 …

    Reply

  20. Microsoft now totally removed the Start Menu from Windows 8 and replaced it with the Start Screen. We decided to do something about it and created a petition to ask Microsoft to bring back the Start Menu. If Microsoft enables the ability for us to choose between the interfaces, then everybody should be happy even those who like the new interface. For this petition to be successful we need a few million signatures; this seems impossible, but can be done. Go to http://www.rizonesoft.com for more information.

    I’m not looking for free traffic to my site, if you could just share the direct petition link that will be perfect and be a tremendous help. Only those who can see the invisible can accomplish the impossible.

    Reply
  24. Pingback: How to enable boot to desktop group policy for Windows 8
  25. Pingback: How to configure a Boot to Desktop Group Policy for Windows 8.1

  26. Good Day I Am So Happy I Found Your Website, I
    Found You By Mistake, While I Was Searching On Aol For
    Something Else, Anyhow I Am Here Now And Would Just Like To Say Many Thanks For
    A Remarkable Post And An All Round Entertaining Blog
    I Don’t Have Time To Read It, All At The Moment But I Have BookMarked It
    And Also Added In Your RSS Feeds, So When I Have Time I Will Be Back To Read More,
    Please Do Keep Up The Fantastic Job.

    Reply

  27. Sometimes when you try to open any web page using its address, you might experience the ERR_SPDY_PROTOCOL_ERROR or might see “This webpage is not available” error appearing on the screen. This is a browser specific error that is faced only by users who use Chrome browser. This error is nothing but a network security issue.

    Reply

Leave a Reply