Posted in Tutorials

How to use Group Policy to Allow or Block URL’s

   08/07/2010  47 Comments



This is another article I have written that address’s the commonly asked question on the Group Policy forum as to how you can use group policy to block or allow users to specific web site URL’s. It goes without saying that the most effective way to implement content filtering for the internet is to maintain list of sites on your proxy server/firewall in your organisation. However you might not have any proxy or firewall that can do this and this method is also not affective when a user is connected to the internet outside the corporate network.

Luckily there is an option in the Internet Explorer Maintenance group policy section that allows you to configured an allow/never list of URL’s for your users. If you are configuring this option I also suggest your also check out one of my other article How to configure AppLocker Group Policy in Windows 7 to block third-party browsers to prevent users from running non-IE browsers to get around this restriction as this is an IE only policy setting.

How to configure Internet Explorer to Allow and Block URL’s

Step 1. Edit a Group Policy Object (GPO) that applies to the users you want to configure URL blocking.

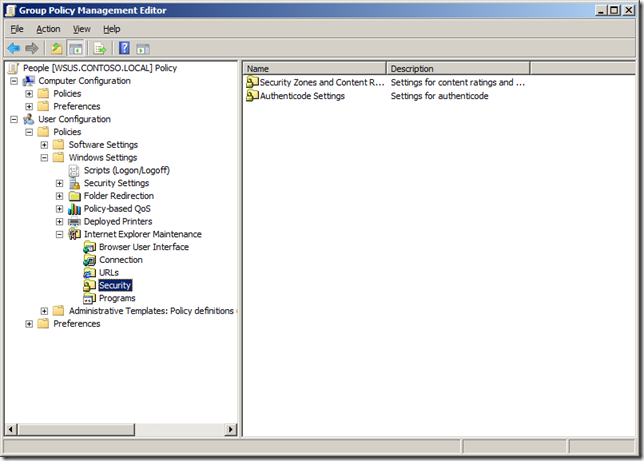
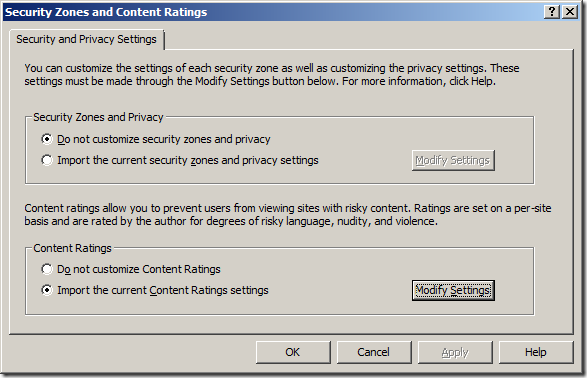
Step 2. Navigate to User Configuration > Policies > Windows Settings > Internet Explorer Maintenance > Security and then click on the “Security Zones and Content Ratings”

image

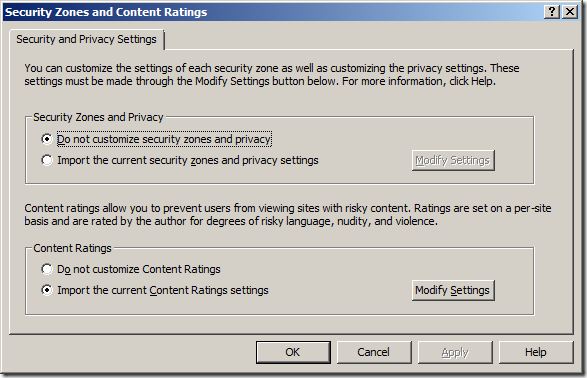
Step 3. Select “Import the current Content Ratings settings” and then click on the “Modify Settings” button

image

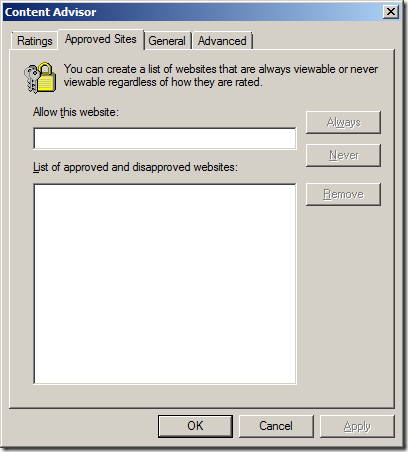
Step 4. Click on the “Approved Sites” tab

image

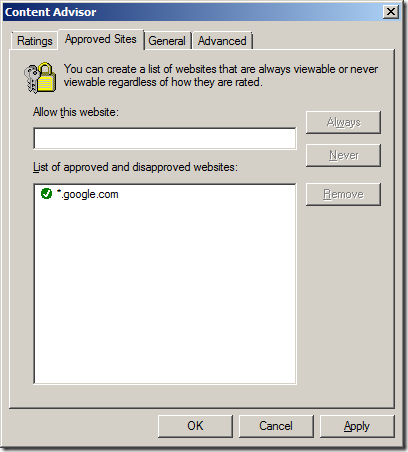
Step 5a (Black List). Type the name of the URL that you want to block in the “Allow this website” text field and then click “Never” then “OK”

image[83]

Step 5b (White List). However if you are trying to maintain a white list of URL’s then type the name of the site you want to allow it the “Allow this website” text field and then click “Always” then “OK”

image

Note: You will probably want to add the internal domain name of your companies AD to the Allow list of as well to ensure users can access the intranet web sites. Also note that while wildcards are supported in the URL’s, but adding just the URL “*” does not work. While this would be very handy to configure a white list I will show you how to get around this restriction in further steps below.

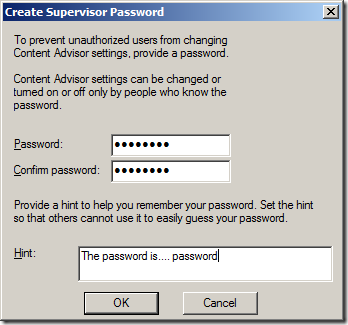
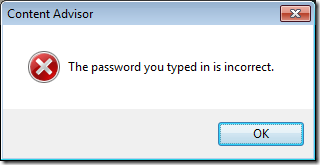
Now we have to create a supervisor password that will be used for making any subsequent changes to the Allow/Never URL list. This password can also be used by the user (if they know it) to work around these URL restrictions. However as this password is applied by policy it will be the same password for all users so think about chancing the password often.

Step 6. Type the same password in both the “Password” and “Confirm Password” fields and type at hint in the “hint” field. You could also type something like “To get this password please contact the help desk on 5555-5555”.

image

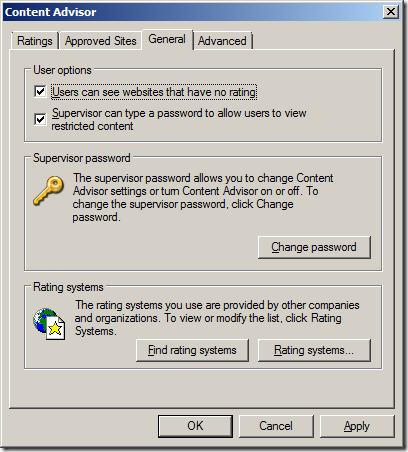
By default when you enable the content advisor it will automatically block any web site that does not have a rating configured.  Therefore you will want to turn this blanket restriction off in step 8 if you all you are trying to do is block specific URL’s in a black list configuration.

Step 8 (Black List). Tick “User can see websites that have no rating” then click “OK”

image

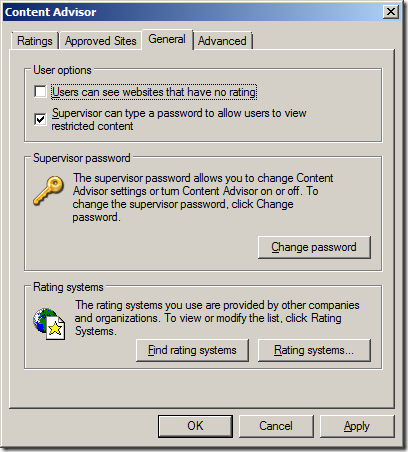
Note: For white list configuration leave the “User can see websites that have no rating” un-ticked so that all web sites will be blocked.

image

Step 9. Click OK

image

Done.

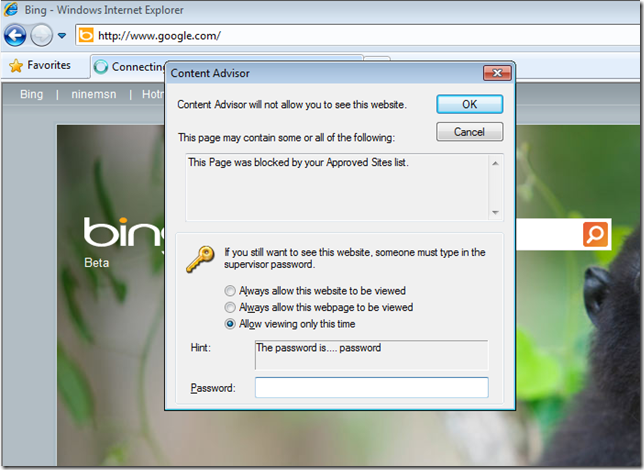
If you configured a black list then a user will be allowed to go to all web sites except the URL that you specifically blocked. When the user does hit a web site that is blocked they will be presented with dialogue box explaining why they are not able to visit the web site and an option to visit the site only if they know the supervisor password.

image

If they click Cancel nothing will happen and if they press OK they will get presented with this dialogue box.

image

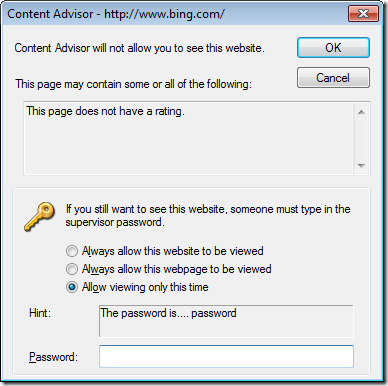
Below is another example message that is presented when visiting a site without a rating and you have configured the policy not load sites that do not have a rating which you will see if you have configured this as a white list.

image

If you are using a white list configured and a users will still be able to visiting as site so long as it is ICRA3 rated and it does not report as having content that falls into any of the rating categories. Therefore this method is not 100% affective for a white list strategy but you do find your users visiting a site that is not specifically allowed then you can simply added it as a blocked URL.

Related Resources:

If you have played with this setting and are looking for a way to remove this setting from the group policy then see my posting How to remove imported Internet Explorer Group Policy Settings

You will also find that the computer you have made these URL restrictions on will now have the supervisor password set (I assume its something about how IEM GPMC interacts with the local computer) so to Remove IE Supervisor Password just delete the HKEY_LOCAL_MACHINE\Software\Microsoft\Windows\Current Version\Policies\Ratings key and it will reset the Content Advisor settings back to defaults.

Author: Alan Burchill

Microsoft MVP (Group Policy)

47 thoughts on “How to use Group Policy to Allow or Block URL’s”

  3. I have done this however while the policy is on the domain and gets applied to the correct users, the settings are tied to the workstation the policy was created on. I discovered that if I removed the policy settings on the local machine, they were erased in the domain policy. In addition while the policy showed on the domain if another administrator tried to edit the policy all they got were the defaults, the list of sites I added were not there…

    Is there a way to do this that won’t tie it to a workstation/server and so that other admins can use MMCs to change it?

    Reply

    1. Good question… I believe this is a quirk with how it is applied so users can work around the restriction. I will let you know if i find out for sure.. .

  4. Is it possible to block a group of websites but allow only a handful of staff (that require access to those sites) to access them?

    Reply

  5. This is the worse advice ever! I implemented this and stalled all the intranet sites and applications!

    Reply

    1. Sorry to hear that it did not work… But i would refere you to this quote in the article… “It goes without saying that the most effective way to implement content filtering for the internet is to maintain list of sites on your proxy server/firewall in your organisation”

  7. Alan, all of our desktops are cookie cutter PCs (meaning they are all of the same model and the hard drives have all be imaged the same). Some managers have asked me to allow only certain websites on some of the PCs. I have been using content advisor to accomplish this. On some PCs, content advisor works perfectly and I can block/allow certain websites; however, on some PCs, content advisor does not work. When I click the enable button, nothing happens. This is very puzzling to me. Can you please tell me why on some PCs the content advisor enable button works and on some other PCs the content advisor enable button does not work. I have check group policy on a PC that works and a PC that doesn’t work, and everything looks the same … am I missing something.

    Reply

  8. Can some body help..
    How can Applocker be applied with time segments i.e. Different policies for different timings..

    Reply

  9. Hi Allan,

    Thanks for the information. That was very helpful…is there a way we can block URL with any domain (for example – Yahoo.com / Yahoo.ca / Yahoo.fr), can I add yahoo.* will it work or is there any other way we can do that, please let me know.

    Reply

  10. I have applied this group policy for content filtering . the thing which is driving nuts is , its prompting password for every website , even if i check mark the “users can see websites that have no rating ” .
    I dont understand this … please help !!

    Reply

  12. Thank you very much for the article. I will go through it and hopefully its applicable in my situation.

    Reply

  13. I found that it only works for Internet Explorer. Is there a way for it to work with all browsers?

    Reply

    1. Sorry… this would only work for Internet Explorer… in fact this option has now been removed from IE10 so it only applies to all IE Browser before IE9…. Best to implement this as a restriction on the proxy server

  14. Actually content advisor is still available in IE 10 ….. It took tons of research but I found out it is still there . You can go about it a couple of ways. You can enable through group policy editor or edit a registry key.

    Group Policy Branch: User Management – Admin Templates – Windows Components – Internet Explorer – Internet Control Panel – Control Panel

    Set Show Content Advisor to enable

    Registry Key: HKEY_CURRENT_USER\Software\Policies\Microsoft\Internet Explorer\Main

    modify ShowContentAdvisor key to 1

    Once your changes are made

    1. open IE 10
    2. from top menu select Internet Options
    3 Select Content Tab
    4. Content Advisor with the option to enable and settings is available

    Reply

  15. Alan, the reason this is happening on the machine you create the policy on is because the IE Maintenance section of the policy is pulling in your local machine when you hit the “Import” button – making changes when you are in there is making those changes to your computer, and then importing when you hit OK. It’s the only part of the GPMC that does this, and I’ve been hoping Microsoft would change it since I started using it back with IE5. For this reason, it’s often a good idea to always make sure you update this section of the GP from a machine that doesn’t have any non-standard IE settings configured, and I usually do a gpupdate /target:user /force before I open it, just to make sure my settings are reset.

    Reply

    1. Hi Chris, I have been experiencing so much difficulty with my GPMC with Internet Explorer 11. Some of my computers running IE11 on the domain are block from the internet which is great but some are not. This has been a problem for months and taking me months of searching for help. Your comment is the closest to what im having problems with. Could you explain in a bit more depth on how I can get my computer which are not pulling the GPMC to act the same way. (If you understand what I mean) Many Thanks Danny

  17. I have win server 2k8 and trying to block a particular site from gpo. I use the step :::: Step 1. Edit a Group Policy Object (GPO) that applies to the users you want to configure URL blocking.
    Step 2. Navigate to User Configuration > Policies > Windows Settings > but after this step , internet explorer maintenance is not showing up…pls help me

    Reply

  23. This does not seem to work in Windows Server 2008 R2 and Winndows 7 clients, I get the “this site has no content rating” blah blah, but when i try to access a website i have blacklisted (facebook, twitter etc), I can access the page no problem…

    Reply

  24. i also tried it and it only worked with internet explorer.even that it is tied to only the workstation to which the policy was set upon.aside that if u have already opened any of the restricted sites already, because the link is still there it can open for you.please what is the best way forward to do this.also i need it badly to implement.

    Reply

  25. Hi i tried this method in my server Windows Server 2008 But nothing get changed. Can u plz help me to block some of websites in my server. I check with many forums and blog everybody says the same that “block the websites using browser” kindly please tell how to do with in server manager…

    Reply

  26. Tell me about:-
    How can we block a website from your computer in all browser without using any software and system host file ?

    Reply

    1. Nice question. I only know of how to block individual PCs on the network without time frame of restriction.

      C:\Windows\System32\drivers\etc
      Then you open hosts file with notepad and edit.

      Example: # 127.0.0.1 http://www.m.facebook.com
      # 127.0.0.1 http://www.facebook.com

      NOTE: In case you cannot save file after editing, right click the file(hosts), select properties, security, Edit and add the account you use to login for this task and give it full right.

      This restrict access irrespective of browser.

      Good luck.

  27. Guys if you want to block the url you have the options here’s how;

    1.HOSTS file
    2.Group Policy
    3.Firewall blocking
    4.Router blocking
    5.3rd party softwares

    Reply

  29. Looking for a Porn Blacklist?

    Our proprietary platform allows us to leverage multiple data sets across the web to pull in new data for the most complete and extensive adult blacklist found anywhere. It gives us a competitive advantage on the competition that allows us to produce an adult blacklist that is second to none.

    —
    Signed,

    Benjamin E. Nichols
    http://www.pornblacklist.com

    Reply

  30. Nice guide. But this cannot treat my request. I need a guide with time frame of restriction period(8:00am-5:30pm).

    Kindly help in case there is a way out.

    Cheers!!!

    Reply

  31. Simple…. Just develop a small app using whatever programming language you want which can edit a .txt file then go to C:\Windows\System32\drivers\etc go on property of the host file…change it so that you can edit it through the app… i forget how to do it but I did it in the past and is possible…then develop the app/script in a way that it cater for time for the edit

    from 8.30-5.30 edit host file to prevent access to http://www.whatever.com then after that edit host file to let it.

    Hope that it helps you.

    David.

    Reply

  33. It blocked all site im visiting even if I checked the “Users can see websites that have no rating”.
    Why?Please help..

    Reply

  36. Hi Sir,
    I want to block accessing porn sites by using windows server 2012R2. I know we can block it by the url of sites. But you know, there are a lot of websites available in the internet.
    So, is any other way to block porn sites by using windows server 2012R2.

    Reply

  37. I need to know about internet Access?

    As My all computers are on domain by name Def.net.local.I am facing an issue that internet is not working on one client of joined domain.Please give me the best possible solution so internet must be in working condition on domain user

    Reply
  38. Pingback: Allow all websites for administrator account and block all websites (but a few) for limited accounts - Boot Panic

Leave a Reply